Estimating Subgroup Heterogeneity in Difference-in-differences

December 2024

This post addresses a common question we have been asked regarding “I have used the Callaway and Sant’Anna” estimator to estimate some average treatment effect for a population, but want to see if the treatment effect varies along different dimensions. This could be for units of different groups like gender, race, or college-degree (discrete $Z_i$ ) or for binned/discretized continuous variables like age-bins (discretized $Z_i$ ). The goal is to estimate the group-time ATT for subgroups defined by a specific $Z_i = z$ for a given value of $z$ .

One way you can think about the Callaway and Sant’Anna approach is that it provides a sort of rubric for how to estimate aggregate parameters: if you can devise a way to estimate an effect for a $(g, t)$ , then the aggregating up the “ $(g,t)$ building blocks” to say an event-study (dynamic) or an overall treatment effect is “standard”.

Brantly has even invested in creating a package, pte, which allows for a “plug-in-play” approach to this. In this package, Brant does all the wiring and you only have to tell it how to estimate the treatment effect for a given $(g, t)$ dataset.

In this post, we will disucss estimating a subgroup-specific $ATT(g,t)$ and then show how to code this in the pte package. A complete example is available in this gist.

Subgroup- $ATT(g,t)$

The basic set-up follows Callaway and Sant’Anna where you observe units treated at different points in time, denoted by $g$ . You are willing to impose that conditional on a vector of baseline characteristics $X_i$ , parallel trends hold:

\mathbb{E}\left( Y_{it}(0) - Y_{i,g-1}(0) \ | \ D_i = 1, X_i \right) = \mathbb{E}\left( Y_{it}(0) - Y_{i,g-1}(0) \ | \ D_i = 0, X_i \right),

Notice this is effectively a selection-on-observables assumption, but instead of $Y_{i}$ , we are looking at the differenced data $Y_{it}(0) - Y_{i,g-1}(0)$ and arguing the mph{change} in untreated $Y$ is independent of $D$ conditional on $X$ .

Then, what the Callaway and Sant’Anna estimator is combine inverse-probability of treatment weighting with a regression adjustment (a so called `doubly-robust’ method). The regression adjustment fits a model using the untreated units $(D_i = 0)$ :

Y_{it}(0) - Y_{i,g-1}(0) = \alpha_0 + X_i \beta_0 + u_i

which predicts changes in $Y(0)$ given $X_i$ . I denote $\alpha$ and $\beta$ with $_0$ to emphasize this is a model for $Y(0)$ . This model can then predict the counterfactaul change in $Y$ for the treated units by plugging in the treated unit’s $X_i$ :

\underbrace{ \mathbb{E}\left( Y_{it}(0) - Y_{i,g-1}(0) \ | \ D_i = 1 \right) }_{\text{Imputed counterfactual}} \approx \frac{1}{N_1} \sum_{i \ : \ D_i = 1} \hat{\alpha}_0 + X_i \hat{\beta}_0

This is then compared to the observed $\frac{1}{N_1} \sum_{i \ : \ D_i = 1} \left( Y_{it} - Y_{i,g-1} \right)$ to form the DID estimate.

For estimating subgroup average effects, we can modify the procedure to take averages of

\left( Y_{it} - Y_{i,g-1} \right) - \left( \hat{\alpha}_0 + X_i \hat{\beta}_0 \right)

for different subgroups defined by $Z_i = z$ .

This procedure is valid if $Z_i$ is one of the covariates you use in your conditional parallel trends assumption (passed in xformla). If you do not include $Z_i$ in $X_i$ , then you are assuming that trends do not vary by $Z_i = z$ which can be a strong assumption (do trends vary by large / smaller counties).

Coding implementation using `pte`

We will use a dataset from the did package of teen employment in 500 counties in the U.S. from 2004 to 2007. The main outcome variable is lemp which is the log of teen employment and the we will look if minimum wage changes have larger or smaller effects in small counties (based on lpop). First, let’s load packages and the dataset.

library(did)
library(pte) # devtools::install_github("bcallaway11/pte")
library(BMisc) # devtools::install_github("bcallaway11/BMisc")
library(fixest)

# Load example minimum wage dataset
data(mpdta, package = "did")

# Discretize population into above and below median
mpdta$large_county <- mpdta$lpop >= quantile(mpdta$lpop, 0.50)

head(mpdta)

    year countyreal     lpop     lemp first.treat treat large_county
866 2003       8001 5.896761 8.461469        2007     1         TRUE
841 2004       8001 5.896761 8.336870        2007     1         TRUE
842 2005       8001 5.896761 8.340217        2007     1         TRUE
819 2006       8001 5.896761 8.378161        2007     1         TRUE
827 2007       8001 5.896761 8.487352        2007     1         TRUE
937 2003       8019 2.232377 4.997212        2007     1        FALSE

The main thing that pte requires of the user is a function to take a dataframe for a given $(g,t)$ and produce a treatment effect estimate. The dataset is effectively your original dataframe subsetted with a few additional variables. To peek under the hood, this is what the data looks like

# NOTE: you do not need to do this, but it's helpful to have an example to test your estimation function on
pte_data <- pte::setup_pte(
  yname = "lemp", gname = "first.treat", tname = "year", idname = "countyreal", data = mpdta
)$data
# g = 2004, t = 2007
gt_data <- two_by_two_subset(pte_data, g = 2, tp = 5)$gt_data

head(gt_data)

     year countyreal     lpop     lemp first.treat treat large_county G    id
2203 2003      13011 2.668755 5.273000           0     0        FALSE 0 13011
2207 2007      13011 2.668755 5.572154           0     0        FALSE 0 13011
2210 2003      13013 3.831767 6.188264           0     0         TRUE 0 13013
2214 2007      13013 3.831767 6.401917           0     0         TRUE 0 13013
2231 2003      13019 2.787169 5.564520           0     0        FALSE 0 13019
2235 2007      13019 2.787169 4.997212           0     0        FALSE 0 13019
            Y .w period name D
2203 5.273000  1      1  pre 0
2207 5.572154  1      5 post 0
2210 6.188264  1      1  pre 0
2214 6.401917  1      5 post 0
2231 5.564520  1      1  pre 0
2235 4.997212  1      5 post 0

Note we have G, id, Y (outcome), .w (weights if provided), period (shifted version of original time), name (pre/post), and D (treatment).

Let’s define our function. This accepts gt_data, the xformla passed, and a custom argument called subgroup which lets you pass an expression to subset the treated group (e.g. large_county == TRUE)

#' Subgroup ATT(g,t) estimation function
#'
#' Leave `subgroup` unspecified (or `NULL` to estimate overall ATT(g,t)
#' Otherwise pass expression to `subgroup` to subset the treated units to a subgroup
#'
did_attgt_subgroup <- function(gt_data, xformla, subgroup = NULL, ...) {
  # convert two period panel into wide with `pre` and `post`
  data_pre <- gt_data[gt_data$name == "pre", ]
  names(data_pre)[names(data_pre) == "Y"] <- "Y_pre"

  data_post <- gt_data[gt_data$name == "post", ]
  names(data_post)[names(data_post) == "Y"] <- "Y_post"
  data_post <- data_post[, c("id", "Y_post")]

  # One row per unit
  wide_data <- merge(data_pre, data_post, by = "id")

  # \Delta Y = Y_{i,t} - Y_{i,g-1}
  wide_data$delta_Y <- wide_data$Y_post - wide_data$Y_pre

  # Fit model using D == 0
  outcome_reg <- fixest::feols(
    fixest::xpd(lhs = "delta_Y", fml = xformla),
    data = wide_data[wide_data$D == 0, ] # never-treated and/or not-yet-treated
  )

  # Predict Y_{it}(0) - Y_{i,g-1}(0) for everyone
  wide_data$delta_Y0_hat <- predict(outcome_reg, newdata = wide_data)

  # Difference between observed delta_y and predicted delta_Y0_hat
  wide_data$diff <- wide_data$delta_Y - wide_data$delta_Y0_hat

  # Get treated units
  treat <- wide_data[wide_data$D == 1, ]

  # Using a little quosure magic to allow `subgroup` to be passed in as an argument
  subgroup <- rlang::enquo(subgroup)
  if (!rlang::quo_is_null(subgroup)) {
    subgroup <- rlang::eval_tidy(subgroup, data = treat)
    treat <- treat[subgroup, ]
  }

  # Estimate ATT for treated units
  attgt <- mean(treat$diff)
  return(list(attgt = attgt))
}

Now, with that function defined we can use it with pte. The function takes very similar arguments to did (variable names and xformla), but requires a few extra arguments (setup_pte_fun and subset_fun) given the extra flexibility given by the pte package.

# Overall ATT
did_res <- pte(
  data = mpdta,
  yname = "lemp",
  gname = "first.treat",
  tname = "year",
  idname = "countyreal",
  xformla = ~lpop,
  setup_pte_fun = pte::setup_pte,
  subset_fun = pte::two_by_two_subset,
  # base_period = "universal",
  biters = 50,
  # No subgroup filter so it estimates an overal ATT(g,t)
  attgt_fun = did_attgt_subgroup
)
summary(did_res)

Overall ATT:  
     ATT    Std. Error     [ 95%  Conf. Int.]  
 -0.0323        0.0127    -0.0572     -0.0073 *


Dynamic Effects:
 Event Time Estimate Std. Error [95% Pointwise  Conf. Band]  
         -3   0.0267     0.0148         -0.0023      0.0558  
         -2  -0.0051     0.0116         -0.0279      0.0176  
         -1  -0.0233     0.0145         -0.0517      0.0051  
          0  -0.0200     0.0125         -0.0446      0.0046  
          1  -0.0550     0.0115         -0.0776     -0.0323 *
          2  -0.1385     0.0357         -0.2085     -0.0685 *
          3  -0.1075     0.0340         -0.1742     -0.0409 *
---
Signif. codes: `*' confidence band does not cover 0

# Check similar results using `did` when using Outcome Regression
did::aggte(
  did::att_gt(
    data = mpdta,
    yname = "lemp",
    gname = "first.treat",
    tname = "year",
    idname = "countyreal",
    xformla = ~lpop,
    est_method = "reg"
  ),
  "dynamic"
)

Call:
did::aggte(MP = did::att_gt(data = mpdta, yname = "lemp", gname = "first.treat", 
    tname = "year", idname = "countyreal", xformla = ~lpop, est_method = "reg"), 
    type = "dynamic")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


Overall summary of ATT's based on event-study/dynamic aggregation:  
     ATT    Std. Error     [ 95%  Conf. Int.]  
 -0.0808        0.0187    -0.1174     -0.0441 *


Dynamic Effects:
 Event time Estimate Std. Error [95% Simult.  Conf. Band]  
         -3   0.0264     0.0142       -0.0097      0.0624  
         -2  -0.0041     0.0130       -0.0371      0.0288  
         -1  -0.0235     0.0146       -0.0607      0.0138  
          0  -0.0211     0.0117       -0.0509      0.0086  
          1  -0.0534     0.0163       -0.0949     -0.0118 *
          2  -0.1411     0.0394       -0.2414     -0.0408 *
          3  -0.1075     0.0332       -0.1921     -0.0230 *
---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Outcome Regression

Now, we can pass the subgroup argument to estimate effects for large counties and for small counties separately.

did_res_Z0 <- pte(
  data = mpdta,
  yname = "lemp",
  gname = "first.treat",
  tname = "year",
  idname = "countyreal",
  xformla = ~lpop,
  setup_pte_fun = pte::setup_pte,
  subset_fun = pte::two_by_two_subset,
  # base_period = "universal",
  biters = 50,
  attgt_fun = did_attgt_subgroup,
  subgroup = (large_county == FALSE)
)
summary(did_res_Z0)

Overall ATT:  
     ATT    Std. Error     [ 95%  Conf. Int.] 
 -0.0301        0.0233    -0.0757      0.0154 


Dynamic Effects:
 Event Time Estimate Std. Error [95% Pointwise  Conf. Band]  
         -3   0.0284     0.0237         -0.0180      0.0748  
         -2  -0.0148     0.0199         -0.0539      0.0243  
         -1  -0.0249     0.0268         -0.0774      0.0277  
          0  -0.0149     0.0222         -0.0583      0.0286  
          1  -0.0902     0.0358         -0.1605     -0.0199 *
          2  -0.2100     0.0534         -0.3147     -0.1054 *
          3  -0.1413     0.0575         -0.2541     -0.0286 *
---
Signif. codes: `*' confidence band does not cover 0

did_res_Z1 <- pte(
  data = mpdta,
  yname = "lemp",
  gname = "first.treat",
  tname = "year",
  idname = "countyreal",
  xformla = ~lpop,
  setup_pte_fun = pte::setup_pte,
  subset_fun = pte::two_by_two_subset,
  # base_period = "universal",
  biters = 50,
  attgt_fun = did_attgt_subgroup,
  subgroup = (large_county == TRUE)
)
summary(did_res_Z1)

Overall ATT:  
     ATT    Std. Error     [ 95%  Conf. Int.]  
 -0.0338        0.0086    -0.0508     -0.0169 *


Dynamic Effects:
 Event Time Estimate Std. Error [95% Pointwise  Conf. Band]  
         -3   0.0255     0.0112          0.0035      0.0474 *
         -2   0.0012     0.0103         -0.0190      0.0213  
         -1  -0.0216     0.0183         -0.0574      0.0142  
          0  -0.0247     0.0085         -0.0413     -0.0081 *
          1  -0.0275     0.0198         -0.0662      0.0113  
          2  -0.0669     0.0203         -0.1066     -0.0272 *
          3  -0.0738     0.0234         -0.1196     -0.0279 *
---
Signif. codes: `*' confidence band does not cover 0

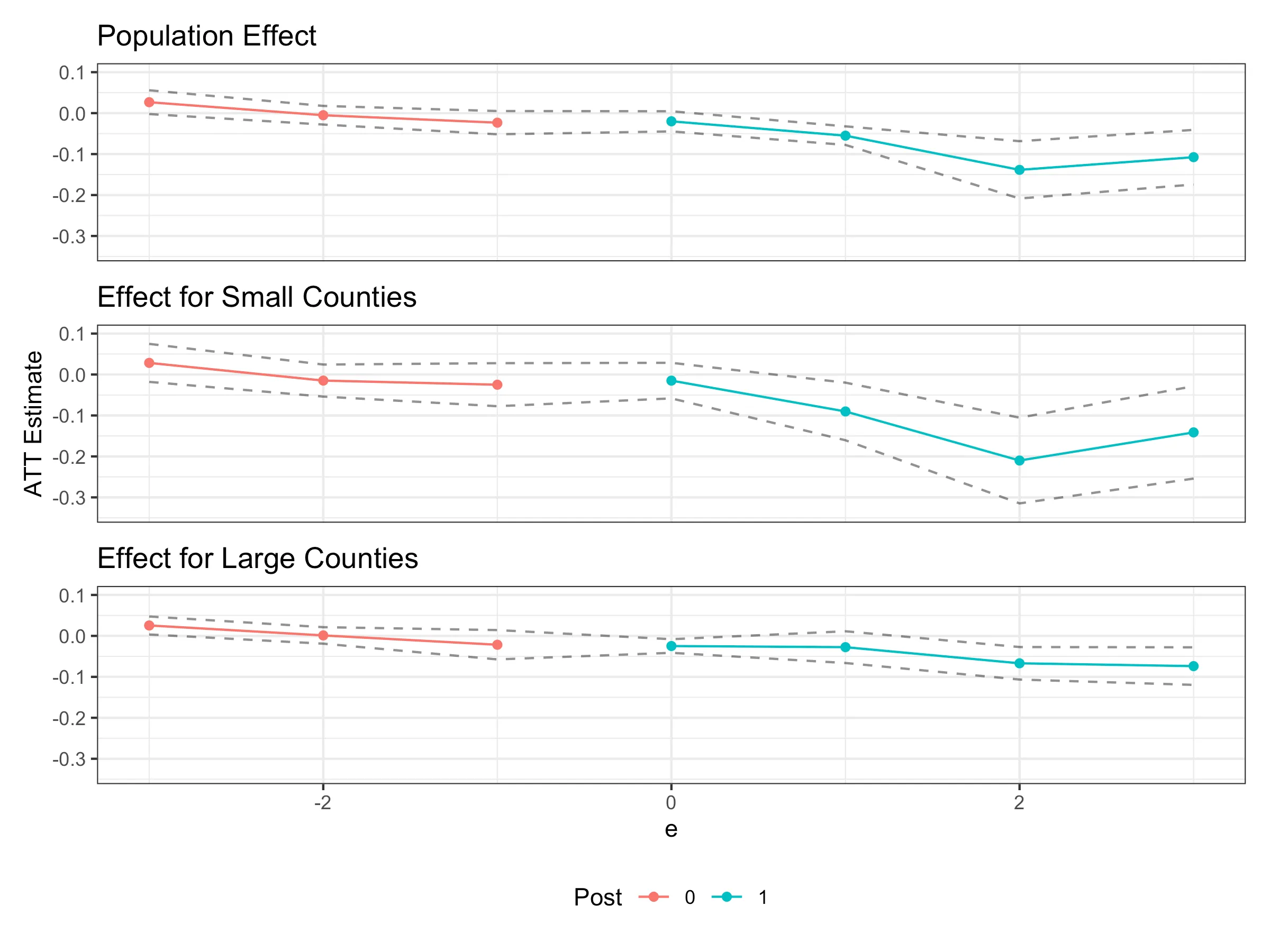
Plotting results

library(ggplot2)
library(patchwork)
plot_overall <- pte:::ggpte(did_res) +
  labs(title = "Population Effect") +
  theme(legend.position = "bottom")

plot_Z0 <- pte:::ggpte(did_res_Z0) +
  labs(title = "Effect for Small Counties") +
  theme(legend.position = "bottom")

plot_Z1 <- pte:::ggpte(did_res_Z1) +
  labs(title = "Effect for Large Counties") +
  theme(legend.position = "bottom")

# Combine figures into one plot
((plot_overall / plot_Z0 / plot_Z1) &
  scale_y_continuous(limits = c(-0.34, 0.1)) &
  labs(y = "ATT Estimate", color = "Post") &
  theme(legend.position = "bottom")
) +
  plot_layout(axes = "collect", guides = "collect")

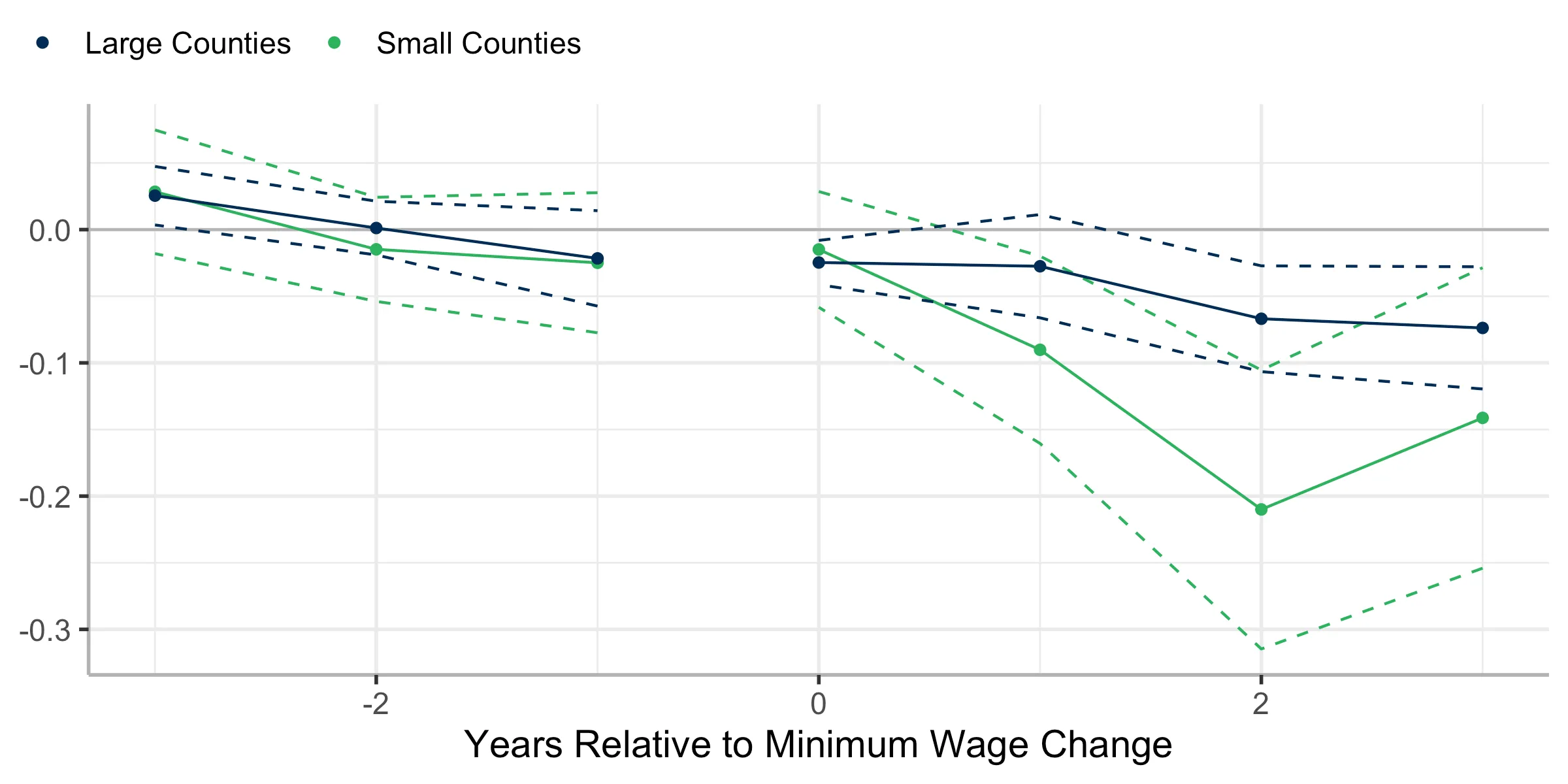
Or, you can extract the event-study estimates directly using summary() and plot the estimates however you wish.

plot_df_Z0 <- summary(did_res_Z0)$event_study
  colnames(plot_df_Z0) <- c("e", "att", "se", "cil", "ciu")
plot_df_Z1 <- summary(did_res_Z1)$event_study
colnames(plot_df_Z1) <- c("e", "att", "se", "cil", "ciu")

ggplot() +
  geom_hline(yintercept = 0, color = "grey70") + 
  geom_line(
    aes(x = e, y = att, color = "Small Counties", group = (e >= 0)),
    data = plot_df_Z0
  ) +
  geom_point(
    aes(x = e, y = att, color = "Small Counties"),
    data = plot_df_Z0
  ) +
  geom_ribbon(
    aes(x = e, ymin = cil, ymax = ciu, color = "Small Counties", group = (e >= 0)),
    data = plot_df_Z0,
    fill = NA, linetype = "dashed"
  ) +
  geom_line(
    aes(x = e, y = att, color = "Large Counties", group = (e >= 0)),
    data = plot_df_Z1
  ) +
  geom_point(
    aes(x = e, y = att, color = "Large Counties"),
    data = plot_df_Z1
  ) +
  geom_ribbon(
    aes(x = e, ymin = cil, ymax = ciu, color = "Large Counties", group = (e >= 0)),
    data = plot_df_Z1,
    fill = NA, linetype = "dashed"
  ) +
  labs(x = "Years Relative to Minimum Wage Change", y = NULL, color = NULL) + 
  scale_color_manual(
    values = c(
      "Large Counties" = "#002C55",
      "Small Counties" = "#2DB25F"
    ),
    guide = guide_legend(override.aes = list(linetype = "blank"))
  ) +
  theme_bw(base_size = 14) +
  theme(
    panel.border = element_blank(), axis.line = element_line(color = "grey70"),
    legend.position = "top", 
    legend.margin = margin(0, 0, 0, 0),
    legend.justification = c(0, 1), 
    legend.location = "plot"
  )

References

Citation:

@online{callaway-unconfoundedness-regressions-2024,
  author       = {Callaway, Brantly},
  title        = {Interpreting Regressions under the Assumption of Unconfoundedness},
  year         = {2024},
  month        = {11},
  url          = {https://bcallaway11.github.io/posts/unconfoundedness-regressions},
  urldate      = {\today},
}

Estimating Subgroup Heterogeneity in Difference-in-differences

Subgroup-ATT(g,t)ATT(g,t)ATT(g,t)

Coding implementation using pte

Plotting results

References

Subgroup- $ATT(g,t)$

Coding implementation using `pte`